Goal: Significally improve peformance of factorial algorithm by leveraging all available processors.

Standard factorial implementation usually looks something like this:

    def factorial(1), do: 1 
    def factorial(n), do: n * factorial(n-1)    

The recursive definition above means that
at the end of the day factorial(5) is going to be translated to 1*2*3*4*5.

Let's make the algorithm parallel. The idea behind it is simple:

• figure out the number of available cores
• divide the work into separate chunks (where number of chunks is equal to number of cores)
• process each piece of work in different Elixir process
• send the results to the parent process
• in the parent process accumulate and multiply the results

An example: Let's say we have 4 cores available and want to calculate a factorial of 20. In this particular scenario the algorithm is going to divide the work into 4 chunks, process each single one of them in a separate Elixir process, notify the parent process when the work is done and multiply the results:

• First process: 1*2*3*4*5 = 120
• Second process: 6*7*8*9*10 = 30240
• Third process: 11*12*13*14*15 = 360360
• Fourth process: 16*17*18*19*20 = 1860480
• Parent process: 120 * 30240 * 360360 * 1860480 = 2432902008176640000

Here is the implementation. First of all let's write some initial tests:

 test "calculate factorial(50) succeeds" do
      assert DistributiveFactorial.calculate_factorial(50) == 30414093201713378043612608166064768844377641568960512000000000000
  end

  test "calculate factorial succeeds 48" do
      assert DistributiveFactorial.calculate_factorial(48)  == 12413915592536072670862289047373375038521486354677760000000000
  end

Let's implement the algorithm now (github repository):

defmodule DistributiveFactorial do  
  def calculate_factorial  n do
    do_calculate_factorial n, items_per_chunk(n), number_of_distributive_chunks        
    collect_the_results([],number_of_distributive_chunks) |> Enum.reduce &(&1*&2)
  end   

  defp do_calculate_factorial  n, _items_per_chunk, 1 do        
    main_pid = self
    spawn fn-> send main_pid, {:factorial_chunk, factorial(n, n)} end
  end

  defp do_calculate_factorial  n, items_per_chunk, counter do
    main_pid = self
    spawn fn-> send main_pid, {:factorial_chunk, factorial(n, items_per_chunk)} end
    do_calculate_factorial n - items_per_chunk , items_per_chunk , counter - 1        
  end

  defp factorial(n, 1), do: n

  defp factorial(n, counter), do: n * factorial(n - 1, counter - 1)

  defp collect_the_results(list, 0), do: list    

  defp collect_the_results(list, counter) do
    receive do 
    {:factorial_chunk,value} -> collect_the_results([value|list], counter - 1) 
    end
  end

  defp items_per_chunk(n), do: div(n, number_of_distributive_chunks)

  defp number_of_distributive_chunks, do: :erlang.system_info(:logical_processors)

end  

Basically we have one public method calculate_factorial, wich takes factorial number n as a parameter. All the others are private helper methods. Under the hood calculate_factorial calls private do_calculate_factorial which divides the work into the chunks and executes it. Later on parent process accumulates the results by calling collect_the_results and multiplies them via Enum.reduce

I went ahead and did some benchmarking, leveraging Benchwarmer package.The result was quite predictable for me though.

My laptop has 4 cores and parallel factorial(400) is being processed for up to 45 seconds according to the benchmark:

Benchwarmer.benchmark fn -> DistributiveFactorial.calculate_factorial 400_000 end

*** #Function<20.90072148/0 in :erl_eval.expr/5> ***
45.9 sec      1 iterations   45915362.0 μs/op  

Non parallel version of factorial is going to take about 180 sec (which is kind of 45 * 4) .

Here is how load is being distributed between processors in the parallel version of factorial:

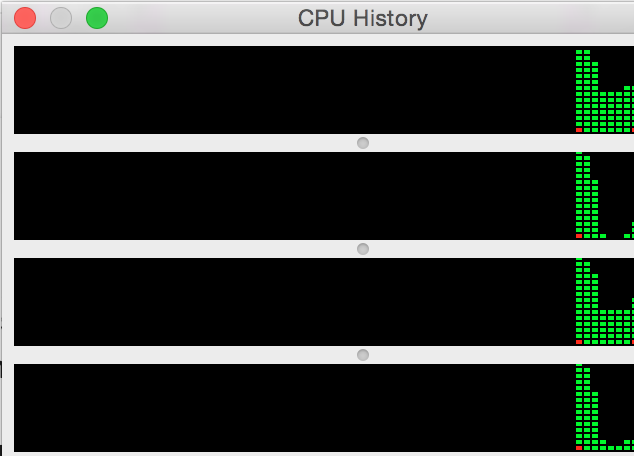
And in the standard one:

In the foreseeable future I'm planning to evolve this particular implementation of the algorithm by making it truly distributive and run all the calculations on different nodes.